При наборе номера телефона, абонент забыл последние 2 цифры, помня лишь, что они разные?
При наборе номера телефона, абонент забыл последние 2 цифры, помня лишь, что они разные.
Сколько существует случаев нахождения номера, который забыл абонент?
Опишите решение пожалуйста.
90 вариантов набора номера.
При наборе телефонного номера абонент забыл последнюю цифру и набрал ее наудачу, помня только то что эта цифра нечетная?
При наборе телефонного номера абонент забыл последнюю цифру и набрал ее наудачу, помня только то что эта цифра нечетная.
Найти вероятность того, что номер набран правильно?
Набирая номер телефона, абонент забыл последние 2 цифр?
Набирая номер телефона, абонент забыл последние 2 цифр.
Какова вероятность того, что он с первого раза наберет эти цифры правильно, если он : а) помнит, что цифры различны, б) ничего не помнит о цифрах, в) помнит, что все цифры четные.
Абонент забыл шестизначный номер телефона и набрал его наугад, помня лишь, что все цифры в нем различны?
Абонент забыл шестизначный номер телефона и набрал его наугад, помня лишь, что все цифры в нем различны.
Какова вероятность набрать нужный номер?
Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу?
Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу.
Найти вероятность того, что набрана нужная цифра.
Набирая номер телефона, абонент забыл три последние цифры, и помня только, что они различны, набрал их наудачу?
Набирая номер телефона, абонент забыл три последние цифры, и помня только, что они различны, набрал их наудачу.
Какова вероятность, что он набрал нужные цифры.
Найти вероятность того, что : а)номер набран правильно с первой попытки ; б)для попадания по нужному номеру понадобиться не более четырех попыток.
Набирая номер телефона, абонент забыл две последние цифры, но помнит, что одна из них – ноль, а другая – нечетная?
Набирая номер телефона, абонент забыл две последние цифры, но помнит, что одна из них – ноль, а другая – нечетная.
Найти вероятность того, что он наберет правильный номер.
Набирая номер телефона абонент забыл две последние цыфры и помня лишь что эти цифры различны набрал их на удачу какова вероятность того что номер набран правильно?
Набирая номер телефона абонент забыл две последние цыфры и помня лишь что эти цифры различны набрал их на удачу какова вероятность того что номер набран правильно?
Какова вероятность того, что набран нужный номер?
Источник
Решение задачи на классическую вероятность
Задача 1: Абонент забыл последнюю цифру номера телефона и поэтому набирает её наугад. Определить вероятность того, что ему придётся звонить не более чем в 3 места.
Решение: Вероятность набрать верную цифру из десяти равна по условию 1/10. Рассмотрим следующие случаи:
Ответ: 0,3
Задача 2: Абонент забыл последние 2 цифры телефонного номера, но помнит, что они различны и образуют двузначное число, меньшее 30. С учетом этого он набирает наугад 2 цифры. Найти вероятность того, что это будут нужные цифры.
m = 1, так как только одно число правильное. Подсчитаем количество всех возможных двузначных чисел с разными цифрами, меньшее 30, которые может набрать абонент: 10 1213 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29. Таких чисел n = 18 штук. Тогда искомая вероятность P=1/18.
Ответ: 1/18.
Задача 3. Шесть шаров случайным образом раскладывают в три ящика. Найти вероятность того, что во всех ящиках окажется разное число шаров, при условии, что все ящики не пустые.
Тогда искомая вероятность P=6/10.
Ответ: 0,6.
Тогда искомая вероятность P=(64*49)/(64*63)=49/63.
Ответ: 49/63.
Подсчитаем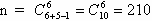 
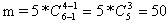
— число различных способов разложить 6 рукописей по 5 папкам, причем в каждой папке может быть любое количество рукописей. Теперь подсчитаем 
— число способов разложить 6 рукописей по 4 папкам, причем в каждой папке должно быть не менее одной рукописи. При этом нужно полученное число сочетаний умножить на 5, так как папку, которая останется пустой, можно выбрать 5 способами. Искомая вероятность Р=50/210=5/21.
Ответ: 5/21.
Случай а). n = 9, так как всего 9 различных карточек. m = 4, так как всего на 4 карточках написаны четные числа (2, 4, 6, 8). Тогда P=4/9.
Случай б). n = 9, так как всего 9 различных карточек. m = 0, так как на всех карточках написаны однозначные числа. Тогда P=0/9=0.
Ответ: 4/9, 0.
Тогда искомая вероятность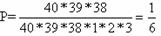 
Ответ: 1/6.
Ответ: 1/120.
Число различных перестановок из букв А, К, К, Л, У равно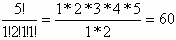 
, из них только одна соответствует слову «кукла» (m=1), поэтому по классическому определению вероятности вероятность того, что ребенок соберет из кубиков слово «кукла» равна P=1/60.
Ответ: 1/60.
Источник
